2020 AMC 10B 试题/第1题
题目
求值
\[ 1 - \left( {-2}\right) - 3 - \left( {-4}\right) - 5 - \left( {-6}\right) ? \]
(A) -20 (B) -3 (C) 3 (D) 5 (E) 21
解答
我们知道减去负数时, \( a - \left( {-b}\right) = a + b \) 。
方程变为 ~quacker88
2020 AMC 10B 试题/第2题
题目
Carl 有5个边长为1的立方体,Kate 有5个边长为2的立方体。这10个立方体的总体积是多少?
(A) 24 (B) 25 (C) 28 (D) 40 (E) 45
解答
边长为1的立方体体积为 \( {1}^{3} = 1 \) ,因此5个的总体积为 \( 5 \cdot 1 = {25} \) 。
边长为2的立方体体积为 \( {2}^{3} = 8 \) ,因此5个的总体积为 \( 5 \cdot 8 = {15} \) 。
\( 5 + {40} = \) (D) \( \sim \) quacker88
2020 AMC 10B 试题/第3题
问题 3
\( w \) 与 \( x \) 的比为 \( 4 : 3 \) , \( y \) 与 \( z \) 的比为 \( 3 : 2 \) ,且 \( z \) 与 \( x \) 的比为 \( 1 : 6 \) 。求 \( w \) 与 \( y \) 的比。
(A) \( 4 : 3 \) (B) \( 3 : 2 \) (C) \( 8 : 3 \) (D) \( 4 : 1 \) (E) \( {16} : 3 \) 解法 1
不失一般性,设 \( w = 4 \) 与 \( x = 3 \) 。
由于 \( z \) 与 \( x \) 的比为 \( 1 : 6 \) ,可将 \( x \) 的值代入得到
\( \frac{z}{3} = \frac{1}{6} \Rightarrow z = \frac{1}{2}. \)
\( y \) 与 \( z \) 的比为 \( 3 : 2 \) ,因此 \( \frac{y}{\frac{1}{2}} = \frac{3}{2} \Rightarrow y = \frac{3}{4} \) 。
于是 \( w \) 与 \( y \) 的比为 \( \frac{4}{\frac{3}{4}} = \frac{16}{3} \) ,所以答案为 \( \left( {\mathbf{E}){16} : 3}\right) \sim \) quacker88
解法 2
我们需要把这三个比联系起来。可以先通过将最后一个比乘以二来连接后两个比。
\( z : x = 1 : 6 = 2 : {12} \) ,又因为 \( y : z = 3 : 2 \) ,可将它们联立得到 \( y : z : x = 3 : 2 : {12} \) 。
最后,由于 \( x : w = 3 : 4 = {12} : {16} \) ,可再次联立得到: \( y : z : x : w = 3 : 2 : {12} : {16} \) ,因此 \( w : y = 1 \) (E) \( {16} : 3 \) ) quacker88
2020 AMC 10B 试题/问题 4
问题
某直角三角形的两个锐角分别为 \( {a}^{ \circ } \) 与 \( {b}^{ \circ } \) ,其中 \( a > b \) ,且 \( a \) 与 \( b \) 均为质数。求 \( b \) 的最小可能值。
(A) 2 (B) 3 (C) 5 (D) 7 (E) 11
解法
因为三角形的三个角之和为 \( {180}^{ \circ } \) ,且这是一个直角三角形,所以其中一个角为 \( {90}^{ \circ } \) ,因此 \( {a}^{ \circ } + {b}^{ \circ } = {90}^{ \circ } \) 。
小于90的最大质数是89。如果 \( a = {89}^{ \circ } \) ,则 \( b = {90}^{ \circ } - {89}^{ \circ } = {1}^{ \circ } \) ,而这不是质数。
小于90的次大质数是83。如果 \( a = {83}^{ \circ } \) ,则 \( b = {7}^{ \circ } \) ,而这是质数,因此我们的答案是 \( \left\lbrack {\left( D\right) 7}\right\rbrack \sim \) quacker88
解法2
观察选项,只有7和11与90互质。测试7会使另一个角为83,而83是质数,因此我们的答案是 \( \left| {\left( \mathrm{D}\right) 7}\right| \)
2020 AMC 10B 试题/第5题
题目
从左到右排成一行,有1块棕色砖、1块紫色砖、2块绿色砖和3块黄色砖,共有多少种可区分的排列方式?(同色砖不可区分。)
(A) 210 (B) 420 (C) 630 (D) 840 (E) 1050
解法
我们先假设所有砖块都可区分,计算可能的排列数,再除以重复计算的部分。
共有 \( 7! \) 种方式排列7个对象。然而,由于黄色砖块不可区分,有 \( 3! = 6 \) 种方式交换它们而不改变排列,绿色砖块也有 \( 2! = 2 \) 种排列方式,因此需要除以这些重复。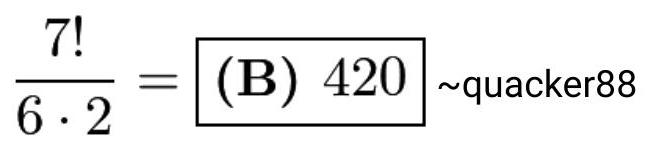
解法
我们可以大量使用组合选择来求出答案。从7个位置中选3个放黄色砖,有C(7,3)=35种方式。然后从剩下的4个位置中选 \( 2 = 6 \) 个放红色砖。最后,在剩下的两个位置中,紫色砖和棕色砖有两种排列方式,因此答案为 \( {35} * 6 * 2 = {420}\frac{7!}{6 \cdot 2} = 6 \) (B) 420 - noahdavid
2020 AMC 10B 试题/第6题
题目
在高速公路上行驶时,梅根注意到她的里程表显示15951(英里)。这个数字是一个回文数——正读反读都一样。2小时后,里程表显示了下一个更大的回文数。在这2小时内,她的平均速度是多少英里每小时?
(A) 50 (B) 55 (C) 60 (D) 65 (E) 70
解答
为了得到大于15951的最小回文数,我们需要将中间的数字加1。如果我们把中间之后的任何一位数字加1,就必须同时把中间之前的一位数字也加1,以保持回文性质,这会使数字不必要地变大。
因此我们将9加1变成10,但显然进位后我们进入了16000区间。为了保持回文,数字现在是16061。
所以梅根行驶了 \( {16061} - {15951} = {110} \) 英里。由于这是在2小时内发生的,她的速度是 \( \frac{110}{2} = 6\mathrm{\;B}{255}\mathrm{{mph}}. \sim \) quacker88
视频解答
https://youtu.be/OHR_6U686Qg
~lceMatrix
2020 AMC 10B 问题/第7题
问题
有多少个小于2020的正偶数且是3的倍数的完全平方数?
(A) 7 (B) 8 (C) 9 (D) 10 (E) 12 解答
任何3的偶数倍都是6的倍数,因此我们需要找出小于2020且是6的倍数的完全平方数。任何我们想要的解都将形如 \( {\left( 6n\right) }^{2} \) ,其中 \( n \) 为正整数。最小可能值在 \( n = 1 \) ,最大在 \( n = 7 \) (此时表达式等于1764)。因此,总共有 \( \left| {\left( \mathrm{A}\right) 7}\right| \) 个可能的数。-PCChess
视频解答
https://youtu.be/OHR_6U686Qg
2020 AMC 10B 问题/第8题
问题
点 \( P \) 和 \( Q \) 位于同一平面,且 \( {PQ} = 8 \) 。在该平面内,点 \( R \) 有多少个位置,使得以 \( P \) 、 \( Q \) 和 \( R \) 为顶点的三角形是面积为12平方单位的直角三角形?
(A) 2 (B) 4 (C) 6 (D) 8 (E) 12
解法1
这里有3种情况:
- \( \mathbf{P} \) 为直角顶点。
- \( \mathbf{Q} \) 为直角顶点。
- 新点为直角顶点。
显然有2个点满足条件,一个位于 \( P \) 正右方,一个位于正左方。我们无需计算具体长度,只需知道这是可能的,确实如此。
用完全相同的推理,这种情况也有2个解。
示意图大致如下。我们知道底边 \( \overline{AB} \) 上的高必须为3,因为面积为12。接下来需验证是否存在满足必要条件的有效三角形。
首先, \( \frac{\overline{BC} \cdot \overline{AC}}{2} = {12} \Longrightarrow \overline{BC} \cdot \overline{AC} = {24} \) 由面积决定。
其次, \( {\overline{BC}}^{2} + {\overline{AC}}^{2} = {64} \) 根据勾股定理。
接下来,需寻找有效解。有多种方法:
识别最小值与最大值:
我们知道 \( {\overline{BC}}^{2} + {\overline{AC}}^{2} = {64} \) 的最小值出现在 \( \overline{BC} = \overline{AC} = \sqrt{24} \) 时。此时方程变为 \( {24} + {24} = {48} \) ,小于64。 \( \overline{BC} = 1,\overline{AC} = {24} \) 。方程变为 \( 1 + {576} = {577} \) ,显然大于64。可得出结论:在 \( \overline{BC} \) 和 \( \overline{AC} \) 之间存在满足勾股定理的值。
由于 \( \overline{BC} \neq \overline{AC} \) ,该三角形非等腰,意味着可将其关于 \( \overline{AB} \) 和/或垂直于 \( \overline{AB} \) 的直线反射,共得到4个三角形。
解法 2
注意线段 \( \overline{PQ} \) 既可以是较短的直角边,也可以是较长的直角边,还可以是斜边。如果它是较短的直角边,那么 \( Q \) 有两个可能的位置满足条件——即位于 \( \overline{PQ} \) 的上方或下方。因此,这种情况有2种可能。类似地,可以发现当 \( \overline{PQ} \) 是
较长的直角边时,
线段的上方或下方。因此,答案是 \( 2 + 2 + 4 = 0 \) (D) 8。
视频解法
https://youtu.be/OHR_6U686Qg
2020 AMC 10B 试题/第9题
题目
有多少个有序整数对(x, y)满足方程 \({x}^{2020} + {y}^{2} = {2y}?\) (A) 1 (B) 2 (C) 3 (D) 4 (E) 无穷多 解法
整理各项并对 \( y \) 配方,得到 \( {x}^{2020} + {\left( y - 1\right) }^{2} = 1 \) 。然后注意到 \( x \) 只能取0、1和-1,因为任何大于1的 \( {x}^{2020} \) 值都会使 \( {\left( y - 1\right) }^{2} \) 项小于0,这是不可能的,因为 \( y \) 必须是实数。因此,将上述 \( x \) 的值代入,得到有序对(0,0)、(1,1)、(-1,1)和(0,2),总共有(D) 4个有序对。
解法 2
将所有项移到左边,我们得到一个关于
\[ {y}^{2} - {2y} + {x}^{2020} = 0 \]
。应用二次公式,我们得到
\[ y = \frac{2 \pm \sqrt{4 - 4 \cdot 1 \cdot {x}^{2020}}}{2} = \frac{2 \pm \sqrt{4\left( {1 - {x}^{2020}}\right) }}{2}. \]
为了使 \( y \) 为实数(根据我们寻找整数解的前提,它必须是实数),我们知道判别式 \( 4\left( {1 - {x}^{2020}}\right) \) 必须非负。因此,
\[ 4\left( {1 - {x}^{2020}}\right) \geq 0 \Rightarrow {x}^{2020} \leq 1 \]
在这里,我们看到必须将不等式拆分为复合不等式,得到 \( - 1 \leq x \leq 1 \) 。
满足此条件的整数只有 \( x \in \{ - 1,0,1\} \) 。将这些值代回二次方程,我们发现 \( x = \{ - 1,1\} \) 都产生判别式为0,这意味着 \( y \) 只有一个解。如果 \( x = \{ 0\} \) ,则判别式非零,因此 \( y \) 有两个解。
因此,答案是 \( 2 \cdot 1 + 1 \cdot 2 = 0 \) (D) 4
~提布利斯
解法3,先求x
将其整理为关于y的二次方程:
\[ {y}^{2} - {2y} + {x}^{2020} = 0 \]
则判别式为
\[ \Delta = 4 - 4{x}^{2020} \]
显然,只有当 \( {x}^{2020} \leq 1 \) 时才会得到实数解,因为它始终为正。于是 \( x = - 1,0,1 \) 。逐一检验:-1和1在2020次幂下结果相同:
\[ {y}^{2} - {2y} + 1 = {\left( y - 1\right) }^{2} = 0 \]
这仅有解1,因此 \( \left( {\pm 1,1}\right) \) 即为解。接下来,若 \( x = 0 \) :
\[ {y}^{2} - {2y} = 0 \]
有两个解,因此为(0,2)和(0,0)
这4个就是全部解,因此选(D) 4
解法4,先求y
将 \( {y}^{2} \) 项移到另一边得到 \( {x}^{2020} = {2y} - {y}^{2} = y\left( {2 - y}\right) \) 。因为对所有 \( x \) 都有 \( {x}^{2020} \geq 0 \) ,所以 \( y\left( {2 - y}\right) \geq 0 \Rightarrow y = 0,1,2 \) 。若 \( y = 0 \) 或 \( y = 2 \) ,则右侧为0,因此 \( x = 0 \) 。当 \( y = 1 \) 时,右侧变为1,因此 \( x = 1, - 1 \) 。我们的解为(0,2)、(0,0)、(1,1)、(-1,1)。共有4个解,故答案为 \( \Delta \mathbf{D}2 \) 。
2020 AMC 10B 试题/第10题
问题10
一个半径为4英寸的四分之三圆扇形(sector)连同其内部区域,可以通过将所示两条半径粘合,卷成一个正圆锥的侧面积。求该圆锥的体积,单位为立方英寸。
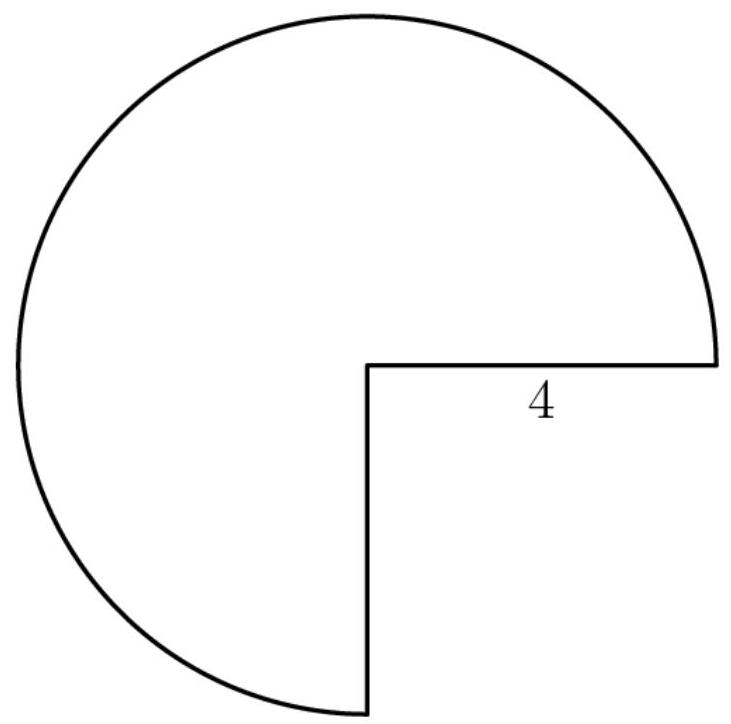
(A) \( {3\pi }\sqrt{5} \) (B) \( {4\pi }\sqrt{3} \) (C) \( {3\pi }\sqrt{7} \) (D) \( {6\pi }\sqrt{3} \) (E) \( {6\pi }\sqrt{7} \)
解决方案
注意,当圆锥被创建时,圆的半径将成为圆锥的斜高(slant height),而圆的完整周长将成为圆锥底面的周长。
我们可以计算出圆的完整周长为 \( {8\pi } \cdot \frac{3}{4} = {6\pi } \) 。由于这也等于圆锥的周长,因此圆锥的半径为3。我们还知道圆锥的斜高为4。因此,我们使用勾股定理(Pythagorean Theorem)计算出圆锥的高度为 \( \sqrt{{4}^{2} - {3}^{2}} = \sqrt{7} \) 。圆锥的体积为
\( \frac{1}{3} \cdot \pi \cdot {3}^{2} \cdot \sqrt{7} = \left( \mathbf{C}\right) {3\pi }\sqrt{7} \cdot \) PCChess
解法2(最后手段/简易法)
用尺子量出一个半径为4的圆,剪下该圆并去掉缺失的四分之一。然后将其折成圆锥,测得直径为 \( 6\mathrm{\;{cm}} \Longrightarrow r = 3 \) 。可以构成一个边长为3、4的直角三角形,再通过勾股定理(Pythagorean theorem)求得高度 \( h \) 为 \( {h}^{2} = {4}^{2} - {3}^{2} \Longrightarrow h = \sqrt{7} \) 。圆锥的体积公式为 \( \frac{1}{3}\pi {r}^{2}h \) 。代入后得到
\[ V = {3\pi }\sqrt{7} \Rightarrow \int \left( \mathbf{C}\right) \]
- DBlack2021
视频解析
https://youtu.be/OHR_6U686Qg(AMC 10)https://youtu.be/6ujfjGLzVoE(AMC 12)
2020 AMC 10B 第11题
题目
Carr女士要求学生从阅读清单上的10本书中任选5本阅读。Harold随机从清单中选出5本,Betty也如此。问他们恰好共同选中2本书的概率是多少?
(A) \( \frac{1}{8} \) (B) \( \frac{5}{36} \) (C) \( \frac{14}{45} \) (D) \( \frac{25}{63} \) (E) \( \frac{1}{2} \)
解答
我们并不关心Harold选了哪些书,只关心Betty从Harold的清单中选了2本,另外3本不在Harold的清单中。
Betty选书的总组合数为 \( \left( \begin{matrix} {10} \\ 5 \end{matrix}\right) = {252} \) 。
Betty从Harold的清单中选2本的方法数为 \( \left( \begin{array}{l} 5 \\ 2 \end{array}\right) = {10} \) 。
在剩下的5本不在Harold清单中的书里,选3本的方法数为 \( \left( \begin{matrix} 5 \\ 3 \end{matrix}\right) = {10} \) 。
视频解析
https://youtu.be/t6yjfKXpwDs
~冰矩阵
2020年AMC 10B试题/第12题
问题
十进制表示
\[ \frac{1}{{20}^{20}} \]
小数点后是一串零,接着是数字9,再后面还有若干位数字。问:小数点后这串零共有多少个?
(A) 23 (B) 24 (C) 25 (D) 26 (E) 27 解法1
\[ \frac{1}{{20}^{20}} = \frac{1}{{\left( {10} \cdot 2\right) }^{20}} = \frac{1}{{10}^{20} \cdot {2}^{20}} \]
现在我们进行估算。注意到 \( {2}^{20} = {1024}^{2} \) ,这意味着 \( {2}^{20} \) 略大于 \( {1000}^{2} = 1,{000},{000} \) 。将其与 \( {10}^{20} \) 相乘,我们得到分母约为 \( 1.{00}\ldots 0 \) 。注意,当我们用1除以一个 \( n \) 位数时,
在第一个非零数字之前有 \( n - 1 \) 个零。这意味着当我们用1除以27位整数 \( 1\underline{0}0\ldots 0 \) 时,小数点后的初始序列中有 \( \left| {\mathbf{\left( D\right) }{26}}\right| \) 个零。——PCChess
解决方案 2
首先将 \( \frac{1}{{20}^{20}} \) 改写为 \( \frac{{5}^{20}}{{10}^{40}} \) 。然后,我们知道当把它写成十进制形式时,小数点后将会有40位数字。因此,我们只需要找出 \( {5}^{20} \) 中的数字个数。
\( \log {5}^{20} = {20}\log 5 \) 和记忆 \( \log 5 \approx {0.69} \) (或者利用 \( \log 5 = 1 - \log 2 \) 这一事实),
\( \lfloor {20}\log 5\rfloor + 1 = \lfloor {20} \cdot {0.69}\rfloor + 1 = {13} + 1 = {14} \) 位数字。
我们的答案是 \( \begin{array}{l} \text{ (D) }{26} \end{array} \)
解法3(暴力枚举)
与解法2一样,我们将 \( \frac{1}{{20}^{20}} \) 改写为 \( \frac{{5}^{20}}{{10}^{40}} \) 。随后我们完全手算 \( {5}^{20} \) :先计算 \( {5}^{5} \cdot {5}^{5} \) ,再将该乘积自乘,得到95,367,431,640,625。由于这是一个14位数,将其连续除以10共14次后,小数点位于9之前。再额外除以10共26次,便可得到一串(D)26|个零。——OreoChocolate
解法4(更聪明的暴力枚举)
与解法2和解法3一样,我们将 \( \frac{1}{{20}^{20}} \) 改写为 \( \frac{{5}^{20}}{{10}^{40}} \) 。接着观察 \( 5,{5}^{1} = 5,{5}^{2} = {25},{5}^{3} = {125},{5}^{4} = {625} \) 、 \( {5}^{5} = {3125} \) 、 \( {5}^{6} = {15625} \) 、 \( {5}^{7} = {78125} \) 等幂的位数。经过几次迭代后我们发现,每当指数为 \( 1{\;\operatorname{mod}\;3} \) 的5的幂,其位数不再增加。这意味着 \( {5}^{20} \) 应有 \( {20} - 6 \) 位,因为从0到20共有6个 \( 1{\;\operatorname{mod}\;3} \) ,总计14位。于是原式可写成 \( \frac{k \cdot {10}^{14}}{{10}^{40}} \) ,其中 \( k \) 落在 \( \lbrack 1,{10}) \) 范围内。约简后得到 \( \frac{k}{{10}^{26}} \) ,即在 \( k \) 前有26个零,因为 \( k \) 应从 \( {10}^{26} \) 中“1”所在的位置开始。~aop2014
视频解析
https://youtu.be/t6yjfKXpwDs
~lceMatrix
2020 AMC 10B 第13题
题目
蚂蚁安迪生活在坐标平面上,当前位于(-20,20),面朝东(即正 \( x \) 方向)。安迪先移动1单位,然后左转 \( {90}^{ \circ } \) 度;接着移动2单位(向北),再左转 \( {90}^{ \circ } \) 度;再移动3单位(向西),再左转 \( {90}^{ \circ } \) 度。安迪继续这一过程,每次移动距离增加1单位,且始终左转。问安迪第2020次左转时所在点的坐标是?
(A)(-1030, - 994) (B)(-1030, - 990) (C)(-1026, - 994) (D)(-1026, - 990)
解法1
可以发现每四步两个坐标各减2。因此两个坐标各需减2共505次。相减后得到答案 \( \left( \mathbf{B}\right) \left( {-{1030}, - {990}}\right) \sim \) happykeeper
另见
2015 AMC 10B 第24题 https://artofproblemsolving.com/wiki/index.php/2015_AMC_10B_Problems/Problem_24
视频解析
2020 AMC 10B 第14题
题目
如下图所示,边长为2的正六边形内部有六个半圆,其直径与六边形的边重合。求阴影区域(位于六边形内部但在所有半圆外部)的面积。
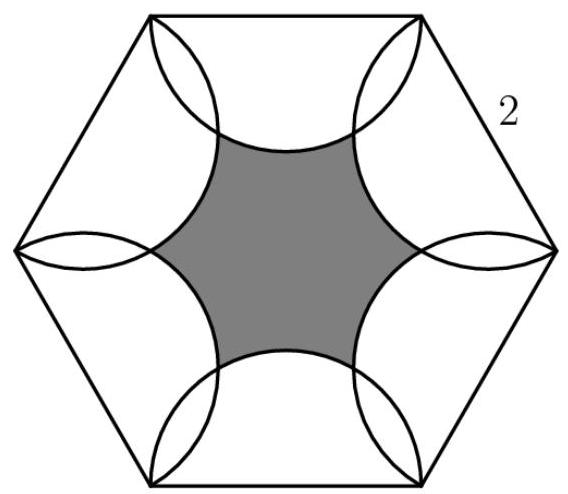
(A) \( 6\sqrt{3} - {3\pi } \) (B) \( \frac{9\sqrt{3}}{2} - {2\pi } \) (C) \( \frac{3\sqrt{3}}{2} - \frac{\pi }{3} \) (D) \( 3\sqrt{3} - \pi \) (E) \( \frac{9\sqrt{3}}{2} - 7 \)
解法1
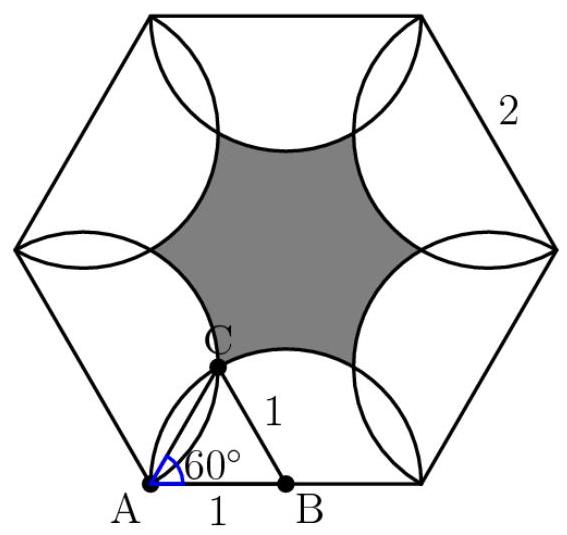
设点A为正六边形的一个顶点,点B为连接点A与其相邻顶点的线段的中点,点C为通过点A的两个半圆的第二个交点。那么, \( {BC} = 1 \) ,因为B是以1为半径且C在其上的半圆的圆心, \( {AB} = 1 \) ,因为B是以1为半径且A在其上的半圆的圆心,而 \( \angle {BAC} = {60}^{ \circ } \) ,因为正六边形的内角为120°,且 \( \angle {BAC} \) 是该六边形中任意角的一半。现在,利用正弦定理, \( \frac{1}{\sin \angle {ACB}} = \frac{1}{\sin {60}^{ \circ }} \) ,因此 \( \angle {ACB} = {60}^{ \circ } \) 。由于三角形内角和为 \( {180}^{ \circ } \) , \( \angle {ABC} \) 也等于 \( {60}^{ \circ } \) 。因此, \( \bigtriangleup {ABC} \) 是一个边长为1的等边三角形。
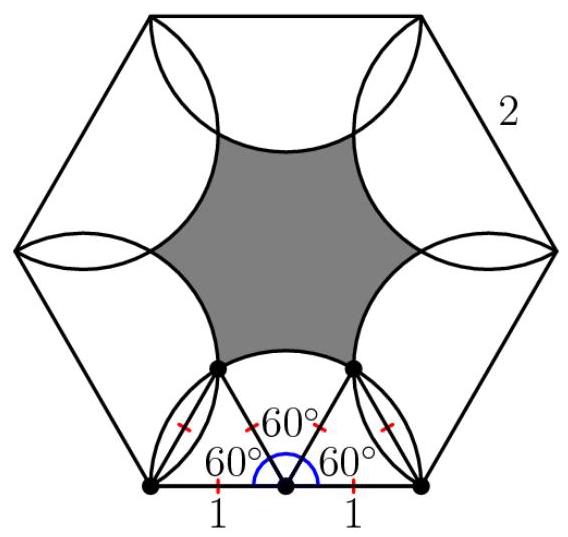
由于正六边形的面积可由公式 \( \frac{3\sqrt{3}{s}^{2}}{2} \) 求得,其中 \( s \) 为六边形的边长,因此该六边形的面积为 \( \frac{3\sqrt{3}\left( {2}^{2}\right) }{2} = 6\sqrt{3} \) 。等边三角形的面积可由公式 \( \frac{\sqrt{3}}{4}{s}^{2} \) 求得,其中 \( s \) 为等边三角形的边长,因此边长为1的等边三角形的面积为 \( \frac{\sqrt{3}}{4}\left( {1}^{2}\right) = \frac{\sqrt{3}}{4} \) 。圆的面积可由公式 \( \pi {r}^{2} \) 求得,因此半径为1的圆的六分之一面积为 \( \frac{\pi \left( {1}^{2}\right) }{6} = \frac{\pi }{6} \) 。在六边形的每一等份中,有两个白色等边三角形,每个面积为 \( \frac{\sqrt{3}}{4} \) ,以及一个半径为1的白色六分之一圆,面积为 \( \frac{\pi }{6} \) 。其余部分为灰色。因此,六边形每一等份中白色部分的总面积为 \( 2\left( \frac{\sqrt{3}}{4}\right) + \frac{\pi }{6} \) ,等于 \( \frac{\sqrt{3}}{2} + \frac{\pi }{6} \) ,而白色部分的总面积为 \( 6\left( {\frac{\sqrt{3}}{2} + \frac{\pi }{6}}\right) \) ,等于 \( 3\sqrt{3} + \pi \) 。由于灰色部分的面积等于六边形总面积减去白色部分面积,因此灰色部分的面积为 \( 6\sqrt{3} - \left( {3\sqrt{3} + \pi }\right) \) ,等于 \( \Delta \left( D\right) 3\sqrt{3} - \pi \) 。
解法2
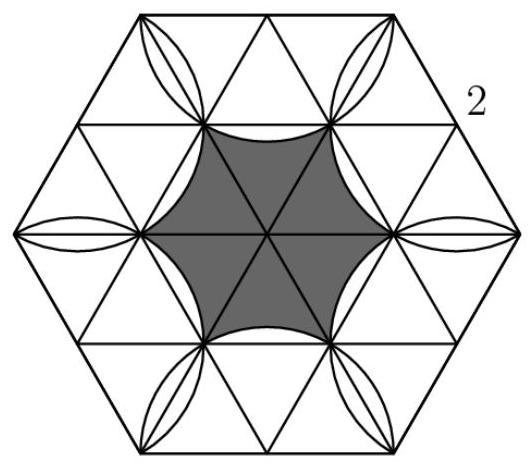
首先,将六边形细分为24个边长为1的等边三角形:
现在注意到整个阴影区域只是该部分的6倍:
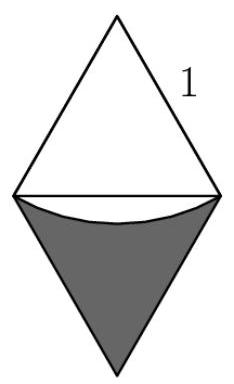
整个菱形只是2个边长为1的等边三角形,因此其面积为:
\[ 2 \cdot \frac{\sqrt{3}}{4} = \frac{\sqrt{3}}{2} \]
未包含在内的弧的面积为:
\[ \frac{1}{6} \cdot \pi \cdot {1}^{2} = \frac{\pi }{6} \]
因此,该部分中阴影区域的面积为
\[ \frac{\sqrt{3}}{2} - \frac{\pi }{6} \]
最终面积为:
\[ 6\left( {\frac{\sqrt{3}}{2} - \frac{\pi }{6}}\right) = 3\sqrt{3} - \pi \Rightarrow \text{ (D) } \]
\( \sim \mathrm{N}{828335} \)
视频解析
https://youtu.be/t6yjfKXpwDs
~lceMatrix
2020 AMC 10B 第15题
题目
史蒂夫按顺序反复写下数字1,2,3,4,5,从左到右构成一个包含10,000位数字的列表,开头为 \( {123451234512}\ldots \) 。接着,他删除列表中每第3位数字(即从左数第3、6、9…位),再删除所得列表中每第4位数字(即剩余列表中从左数第4、8、12…位),最后删除此时剩余列表中每第5位数字。问:此时位于第2019、2020、2021位的三个数字之和是多少?(A) 7 (B) 9 (C) 10 (D) 11 (E) 12
解法1
删除每第3位数字后,列表变为 \( {1245235134}\ldots \) 循环。再从此列表中删除每第4位数字,列表变为 \( {124235341452513}\ldots \) 循环。最后从此列表中删除每第5位数字,列表变为 \( {124253415251}\ldots \) 循环。由于该列表每12位循环一次,且2019、2020、2021在 \( \;\left( {\;\operatorname{mod}\;{12}}\right) , \) 中分别对应3、4、5位,因此第2019、2020、2021位数字分别是第3、4、5位数字。故答案为 \( 4 + 2 + 5 = \) (D) 11。delphin 7
视频解析
https://youtu.be/t6yjfKXpwDs
~lceMatrix
2020 AMC 10B 第16题
题目
贝拉和珍在实数轴上的闭区间 \( \left\lbrack {0, n}\right\rbrack \) 上进行如下游戏,其中 \( n \) 为大于4的固定整数。两人轮流行动,贝拉先手。贝拉第一步可在区间 \( \left\lbrack {0, n}\right\rbrack \) 内任选一实数。此后,轮到的一方需选择一个与双方此前已选所有数字距离均大于1的实数。无法选出该数字者判负。若双方均采用最优策略,哪位玩家将获胜?
(A) 贝拉将始终获胜。 (B) 珍将始终获胜。 (C) 当且仅当 \( n \) 为
(D) 当且仅当 \( n \) 为奇数时,珍获胜。 (E) 当且仅当 \( n > 8 \) 时,珍获胜。
解答
注意,为了使用最优策略赢得游戏,Bela 必须在该区间 \( \left\lbrack {0, n}\right\rbrack \) 中选择中间的数,然后对 Jenn 所选的任何数进行镜像回应。因此,只要 Jenn 能在区间内选一个数,Bela 也能选。Jenn 总会是第一个无数可选的人,所以答案是 (A) Bela 将永远获胜
解法 2(猜测)
首先,要意识到 \( n \) 的取值对策略毫无影响。因为他们可以选实数而非整数,所以即使 \( n \) 是奇数,他们仍可取中点。同理,当 \( n > 8 \) 时,策略也没有理由改变。
于是只剩下 (A) 和 (B)。此时最好随机试几个数,寻找能让 Bela 获胜的策略;若找不到,就意识到答案更可能是 \( \left| {\mathbf{A})\text{Bela will always win}}\right| \) ,因为 Bela 先手,拥有更多主动权。
视频解法
https://youtu.be/3BvJeZU3T-M
~lceMatrix
2020 AMC 10B 问题/第17题
问题
有10个人等距围成一圈。每个人恰好认识其余9人中的3人:站在其左右两侧的2人,以及正对面的人。问:这10个人分成5对,使得每对中的两人都互相认识,共有多少种分法?
(A) 11 (B) 12 (C) 13 (D) 14 (E) 15
解答
我们按对角线的数量进行分情况讨论。
情况1:0条对角线 共有2种方式:要么1与2配对,3与4配对,以此类推;要么10与1配对,2与3配对,等等。
情况2:1条对角线 有5条可能的对角线可画(其余人则与相邻者配对)。
注意,不可能出现2条对角线。
情况3:3条对角线
注意,不可能出现4条对角线的情况,因为那样就必须为剩下的两人再画5条对角线,导致矛盾。
情况4:5条对角线 只有1种方式。
因此,总共有 \( 2 + 5 + 5 + 1 = {13} \) 种可能的方式。
视频解答
https://youtu.be/3BvJeZU3T-M
2020 AMC 10B 问题/第18题
问题
一个瓮里有一红一蓝两个球,旁边有一盒额外的红球和蓝球。乔治重复以下操作四次:他随机从瓮中抽出一球,然后从盒子里取一个同色球,把这两个同色球一起放回瓮中。四次操作后,瓮里共有六个球。问瓮中恰好三红三蓝的概率是多少?
(A) \( \frac{1}{6} \) (B) \( \frac{1}{5} \) (C) \( \frac{1}{4} \) (D) \( \frac{1}{3} \) (E) \( \frac{1}{2} \)
解答
用 \( R \) 表示乔治抽到红球, \( B \) 表示抽到蓝球。为了最终每种颜色各有3球,他还需要各增加2个 \( R \) 和 \( B \) 。
共有6种情况:
\( {RRBB},{RBRB},{RBBR},{BBRR},{BRBR},{BRRB} \) (可以验证只有6种,因为 \( \left( \begin{array}{l} 4 \\ 2 \end{array}\right) = 6 \) )。不过由于对称性, \( {RRBB},{RBRB},{RBBR},{BBRR},{BRBR},{BRRB} \) 、 \( \left( \begin{array}{l} 4 \\ 2 \end{array}\right) = 6 \) 和
\( {RRBB} + {BBRR} \) 、 \( {RBR}\grave{B}\acute{ + }{BRBR} \) 和 \( {RBBR} + {BRRB} \) 可归为一类,因为它们对称等价。
情况1: \( {RRBB} \) 和 \( {BBRR} \)
我们计算他按 \( {RRBB} \) 顺序取球的概率。
第一次抽到红球的概率是 \( \frac{1}{2} \) 。
此时瓮中有2红1蓝,再抽到红球的概率变为 \( \frac{2}{3} \) 。
现在瓮中有3红1蓝,抽到蓝球的概率是 \( \frac{1}{4} \) 。
最后瓮中有3红2蓝,再抽到蓝球的概率是 \( \frac{2}{5} \) 。因此 \( {RRBB} \) 情况发生的概率为 \( \frac{1}{2} \cdot \frac{2}{3} \cdot \frac{1}{4} \cdot \frac{2}{5} = \frac{1}{30} \) 。由于 \( {BBRR} \) 情况对称相同,情况1的总概率为 \( \frac{1}{30} \cdot 2 = \frac{1}{15} \) 。
情况2: \( {RBRB} \) 和 \( {BRBR} \)
我们计算他按 \( {RBRB} \) 顺序取球的概率。
第一次抽到红球的概率是 \( \frac{1}{2} \) 。
现在瓮中有2个红球和1个蓝球。他抽到蓝球的概率是 \( \frac{1}{3} \) 。
现在有2个红球和2个蓝球。他抽到红球的概率是 \( \frac{1}{2} \) 。
最后,有3个红球和2个蓝球。他抽到蓝球的概率是 \( \frac{2}{5} \) 。
因此, \( {RBRB} \) 情况发生的概率是 \( \frac{1}{2} \cdot \frac{1}{3} \cdot \frac{1}{2} \cdot \frac{2}{5} = \frac{1}{30} \) 。
然而,由于 \( {BRBR} \) 情况通过对称性完全相同,情况2发生的概率为 \( \frac{1}{30} \cdot 2 = \frac{1}{15} \) 。
情况3: \( {RBBR} \) 和 \( {BRRB} \)
我们来计算他按 \( R{BBR} \) 顺序抽球的概率。
他第一次抽到红球的概率是 \( \frac{1}{2} \) 。
现在瓮中有2个红球和1个蓝球。他抽到蓝球的概率是 \( \frac{1}{3} \) 。
现在有2个红球和2个蓝球。他抽到蓝球的概率是 \( \frac{1}{2} \) 。
最后,有2个红球和3个蓝球。他抽到红球的概率是 \( \frac{2}{5} \) 。
因此, \( {RBBR} \) 情况发生的概率是 \( \frac{1}{2} \cdot \frac{1}{3} \cdot \frac{1}{2} \cdot \frac{2}{5} = \frac{1}{30} \) 。然而,由于 \( {BRBR} \) 情况通过对称性完全相同,情况3发生的概率为 \( \frac{1}{30} \cdot 2 = \frac{1}{15} \) 。
将所有情况相加,我们得到 \( \frac{1}{15} + \frac{1}{15} + \frac{1}{15} = 1 \) (B) \( \frac{1}{5} \) )-quacker88
解法2
我们知道需要计算按某种顺序添加2个红球和2个蓝球的概率。共有6种方式,因为 \( \left( \begin{array}{l} 4 \\ 2 \end{array}\right) = 6 \) 种排列方式
\( {RRBB} \) 的某种顺序。我们将证明这6种方式的概率相同。
我们首先注意到,所有分母应当用同一个数计数。这个数是 \( 2 \cdot 3 \cdot 4 \cdot 5 = {120} \) 。这是因为2、3、4、5分别代表四步中每一步的可选数量。无论 \( k - {th} \) 步涉及什么,都有 \( k + 1 \) 个数可供选择。
分子是成功操作的次数。无论顺序如何,第一次加入红球时只有1种选择,第二次加入红球时有2种选择,因为最初罐子里只有这么多红球。蓝球同理。分子必须等于 \( {\left( 1 \cdot 2\right) }^{2} \) 。
因此, \( {RRBB} \) 的每种排列的概率都是 \( \frac{4}{120} = \frac{1}{30} \) 。
共有6种情况,所以总概率为 \( \delta \leq 0. \) 解法3
首先注意,乔治每次取球后都会再放回一个同色球。乔治第一次取球时,有 \( \frac{1}{2} \) 的概率取红球,也有 \( \frac{1}{2} \) 的概率取蓝球。我们可以假设他先取 \( \operatorname{Red}\left( {\text{chance}\frac{1}{2}}\right) \) ,然后利用对称性把最终答案乘以2。此时罐子里有两红一蓝。接下来,他要么再取红球(概率 \( \frac{2}{3} \) ),此时必须再取两次蓝球才能各得三球,概率为 \( \frac{1}{4} \cdot \frac{2}{5} = \frac{1}{10} \) ;要么取蓝球,使罐子里变成两红两蓝,概率为 \( \frac{1}{3} \) 。若下一步取蓝球,则他可以先红后蓝或先蓝后红,每种情况概率为 \( \frac{1}{2} \cdot \frac{2}{5} \) ,合计 \( 2 \cdot \frac{1}{5} = \frac{2}{5} \) 。最终得到三红三蓝的总概率为 \( 2 \cdot \frac{1}{2}\left( {\frac{2}{3} \cdot \frac{1}{10} + \frac{1}{3} \cdot \frac{2}{5}}\right) = \frac{1}{15} + \frac{2}{15} = 0 \) 。
解法4
设最终罐中红球更多的概率记为 \( P\left( R\right) \) 。由于这与蓝球更多的概率相等,因此数量相等的概率为 \( 1 - {2P}\left( R\right) \) 。 \( P\left( R\right) = \) 不再选蓝球的概率加上仅再选一次蓝球的概率。第一种情况,
\( P\left( \text{no more blues}\right) = \frac{1}{2} \cdot \frac{2}{3} \cdot \frac{3}{4} \cdot \frac{4}{5} = \frac{1}{5} \) .
第二种情况, \( P\left( {1\text{ more blue }}\right) = 4 \cdot \frac{1 \cdot 1 \cdot 2 \cdot 3}{2 \cdot 3 \cdot 4 \cdot 5} = \frac{1}{5} \) 。因此,
答案为 \( 1 - 2\left( {\frac{1}{5} + \frac{1}{5}}\right) = 1 - \frac{4}{5} = O\left( B\right) \frac{1}{5} \) 。
~JHawk0224
解法5
根据条件概率,4轮后共有5种情况:RRRBBB、RRRRBB、RRBBBB、RRRRRB和RBBBBB。因此概率为 \( \frac{1}{5} \) 。令 \( B \) 。
~FANYUCHEN20020715
由Kinglogic编辑
解法6
这里X代表R或B,Y代表另一种颜色。3轮后可能得到4+1结构(XXXXY),或3+2结构(XXXYY)。从XXXYY到达XXXYYY的概率为 \( \frac{2}{5} \) 。注意到到达4+1结构的概率是
\[ \frac{2}{3} \cdot \frac{3}{4} = \frac{1}{2} \]
\( \left( {\frac{2}{3}\text{to get from XXY to XXXY,}\frac{3}{4}}\right. \) 从 XXXY 变为 XXXXY)。因此,最终得到 3+2 配置的概率也是 \( \frac{1}{2} \) ,答案即为
\[ \frac{1}{2} \cdot \frac{2}{5} = {\left( \text{ B } \cdot \right) }^{\frac{1}{5}}. \]
解法 7
我们可以尝试用动态规划来解决这个问题。(信息学奥林匹克,哈哈)
令 \( {dp}\left\lbrack i\right\rbrack \left\lbrack j\right\rbrack \) 表示最终得到 \( i \) 个红球和 \( j \) 个蓝球的概率。注意,最终得到 \( i \) 个红球和 \( j \) 个蓝球只有两种途径:一种是在罐中有 \( i - 1 \) 个红球和 \( j \) 个蓝球时取出一个红球;另一种是在罐中有 \( i \) 个红球和 \( j - 1 \) 个蓝球时取出一个蓝球。
于是我们有
\[ {dp}\left\lbrack i\right\rbrack \left\lbrack j\right\rbrack = \frac{i - 1}{i - 1 + j}{dp}\left\lbrack {i - 1}\right\rbrack \left\lbrack j\right\rbrack + \frac{j - 1}{i - 1 + j}{dp}\left\lbrack i\right\rbrack \left\lbrack {j - 1}\right\rbrack \]
然后我们可以从 \( {dp}\left\lbrack 1\right\rbrack \left\lbrack 1\right\rbrack = 1 \) 开始,尝试计算 \( {dp}\left\lbrack 3\right\rbrack \left\lbrack 3\right\rbrack \) 。
| \( i \smallsetminus j \) | 1 | 2 | 3 |
| 1 | 1 | 1/2 | 1/3 |
| 2 | 1/2 | 1/3 | 1/4 |
| 3 | 1/3 | 1/4 | 1/5 |
答案是
(CircleOO 的解法)
视频解析
https://youtu.be/3BvJeZU3T-M
~lceMatrix
2020 AMC 10B 第 19 题
题目
在一款纸牌游戏中,玩家从 52 张不同的牌中发到 10 张手牌。可以发给玩家的不同(无序)手牌数可写作 \( {158A00A4AA0} \) 。问数字 \( A \) 是多少?
(A) 2 (B) 3 (C) 4 (D) 6 (E) 7
解法 1
\( {158A00A4AA0} \equiv 1 + 5 + 8 + A + 0 + 0 + A + 4 + A + A + 0 \equiv {4A}\left( {\;\operatorname{mod}\;9}\right) \)
我们要求的是从 52 张牌中选出 10 张的方式数,即 \( \left( \begin{array}{l} {52} \\ {10} \end{array}\right) \) 。
\[ \left( \begin{array}{l} {52} \\ {10} \end{array}\right) = \frac{{52} \cdot {51} \cdot {50} \cdot {49} \cdot {48} \cdot {47} \cdot {46} \cdot {45} \cdot {44} \cdot {43}}{{10} \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \]
我们需要去掉 3 的倍数,这样也会去掉 9 的倍数(否则零会干扰计算,因为不能除以 0)。
\( 9 \cdot 5 = {45},8 \cdot 6 = {48},\frac{51}{3} \) 得到 17。
\[ \frac{{52} \cdot {51}^{17} \cdot {50} \cdot {49} \cdot {48} \cdot {47} \cdot {46} \cdot {45} \cdot {44} \cdot {43}}{{10} \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \]
将其转换为 \( \left( {\;\operatorname{mod}\;9}\right) \) ,我们有
\[ {(\frac{52}{10})} \equiv \frac{( - 2) \cdot ( - 1) \cdot ( - 4) \cdot 4 \cdot 2 \cdot 1 \cdot ( - 1) \cdot ( - 2)}{1 \cdot ( - 2) \cdot 4 \cdot 2 \cdot 1} \equiv ( - 1) \cdot ( - 4) \cdot ( - 1) \cdot ( - 2) \equiv 8\;({mod}\;9 \]
\( {4A} \equiv 8\left( {\;\operatorname{mod}\;9}\right) \Rightarrow A = 4 \) (A) \( 2 \sim \) quacker88
解法 2
\[ {(\frac{52}{10})} = \frac{{52} \cdot {51} \cdot {50} \cdot {49} \cdot {48} \cdot {47} \cdot {46} \cdot {45} \cdot {44} \cdot {43}}{{10} \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = {26} \cdot {17} \cdot 5 \cdot 7 \cdot {47} \cdot {46} \cdot {11} \cdot {43} \]
因为这个数能被 4 整除但不能被 8 整除,所以最后两位必须能被 4 整除,但最后三位不能被 8 整除。这样就把选项缩小到 2 和 6。
此外,该数不能被3整除。将各位数字相加,得到 \( {18} + {4A} \) 。若 \( A = 6 \) ,则该式等于42,是3的倍数。这意味着整个数可被3整除,不符合要求。因此,唯一的选择是 \( \left( \mathbf{A}\right) 2 \) -PCChess
解决方案 3
不难验证13整除该数,
\[ \left( \begin{array}{l} {52} \\ {10} \end{array}\right) = \frac{{52} \cdot {51} \cdot {50} \cdot {49} \cdot {48} \cdot {47} \cdot {46} \cdot {45} \cdot {44} \cdot {43}}{{10} \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = {26} \cdot {17} \cdot 5 \cdot 7 \cdot {47} \cdot {46} \cdot {11} \cdot {43}. \]
作为 \( {10}^{3} \equiv - 1\left( {\;\operatorname{mod}\;{13}}\right) \) ,使用 \( \left( {\;\operatorname{mod}\;{13}}\right) \) 我们得到 \( {13}\left| {\overline{AA0} - \overline{0A4} + \overline{8A0} - \overline{15} = {110A} + {781}}\right| \) 。因此 \( {6A} + 1 \equiv 0{\;(\operatorname{mod}\;{13})} \) ,这意味着 \( A \equiv 2{\;(\operatorname{mod}\;{13})} \) ,所以答案是 \( \left\lbrack {\left( \mathbf{A}\right) 2}\right\rbrack \) 。
数学大师
解决方案 4
如上所述,
\[ \left( \begin{array}{l} {52} \\ {10} \end{array}\right) = \frac{{52} \cdot {51} \cdot {50} \cdot {49} \cdot {48} \cdot {47} \cdot {46} \cdot {45} \cdot {44} \cdot {43}}{{10} \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = {10} \cdot {17} \cdot {13} \cdot 7 \cdot {47} \cdot {46} \cdot {11} \cdot {43} = {158A00A4AA0}. \]
我们可以将 \( {10} \cdot {17} \cdot {13} \cdot 7 \cdot {47} \cdot {46} \cdot {11} \cdot {43} = {158A00A4AA0} \) 两边同时除以10,得到
\[ {17} \cdot {13} \cdot 7 \cdot {47} \cdot {46} \cdot {11} \cdot {43} = {158A00A4AA}, \]
这意味着 \( A \) 就是左侧的个位数。该值为
\[ 7 \cdot 3 \cdot 7 \cdot 7 \cdot 6 \cdot 1 \cdot 3 \equiv \text{(A) 2 (mod 10).} \]
~i_equal_tan_90,由emerald_block修订
视频解析
https://youtu.be/3BvJeZU3T-M
2020 AMC 10B 试题/第20题
问题
设 \( B \) 为一个边长分别为1、3、4的直棱柱(长方体)及其内部。对于实数 \( r \geq 0 \) ,令 \( S\left( r\right) \) 为三维空间中与 \( B \) 中某点距离不超过 \( r \) 的所有点构成的集合。 \( S\left( r\right) \) 的体积可表示为 \( a{r}^{3} + b{r}^{2} + {cr} + d \) ,其中 \( a, b, c, \) 和 \( d \) 为正实数。求 \( \frac{bc}{ad}? \)
(A) 6 (B) 19 (C) 24 (D) 26 (E) 38 解答
将 \( S\left( r\right) \) 划分为4个区域:
- 长方体本身
- \( B \) 各面的延伸
- \( B \) 每条棱处的四分之一圆柱
- \( B \) 每个顶点处的八分之一球
- \( {AC} : 1 + y + x = 2\sqrt{2} \Rightarrow x = \left( {2\sqrt{2} - 1}\right) - y \) 的长度
- CMIF面积: \( \frac{1}{2}{x}^{2} + {xy} = \frac{1}{2} \Rightarrow x\left( {x + {2y}}\right) = 1 \) 。
区域1: \( B \) 的体积为12,因此 \( d = {12} \)
区域2:体积等于 \( B \) 的表面积乘以 \( r \) 。表面积可算得 \( 2\left( {4 * 3 + 3 * 1 + 4 * 1}\right) = {38} \) ,因此 \( c = {38} \) 。
区域3:每个四分之一圆柱的体积等于 \( \left( {\pi * {r}^{2} * h}\right) /4 \) 。所有这类圆柱的体积之和应等于 \( \left( {\pi * {r}^{2}}\right) /4 \) 乘以棱长总和。该总和可算得 \( 4\left( {4 + 3 + 1}\right) = {32} \) ,因此所有四分之一圆柱的体积之和为 \( {8\pi } * {r}^{2} \) ,于是 \( b = {8\pi } \)
区域4:每个顶点处有一个半径为 \( r \) 的八分之一球。由于共有8个顶点,它们拼成一个半径为 \( r \) 的完整球。该球的体积为 \( \frac{4}{3}\pi * {r}^{3}, \) ,因此 \( a = \frac{4\pi }{3}. \)
利用这些值, \( \frac{\left( {8\pi }\right) \left( {38}\right) }{\left( {{4\pi }/3}\right) \left( {12}\right) } = 0\mathbf{\beta }{19} \)
~DrJoyo
视频解析
https://youtu.be/3BvJeZU3T-M
2020 AMC 10B 第21题
题目
在正方形 \( {ABCD} \) 中,点 \( E \) 和 \( H \) 分别位于 \( \overline{AB} \) 和 \( \overline{DA} \) 上,使得 \( {AE} = {AH}. \) 。点 \( F \) 和 \( G \) 分别位于 \( \overline{BC} \) 和 \( \overline{CD} \) 上,点 \( I \) 和 \( J \) 位于 \( \overline{EH} \) 上,使得 \( \overline{FI} \bot \overline{EH} \) 且 \( \overline{GJ} \bot \overline{EH} \) 。见下图。三角形 \( A{EH} \) 、四边形 \( {BFIE} \) 、四边形 \( {DHJG} \) 和五边形 \( {FCGJI} \) 的面积均为1。求 \( F{I}^{2} \) ?
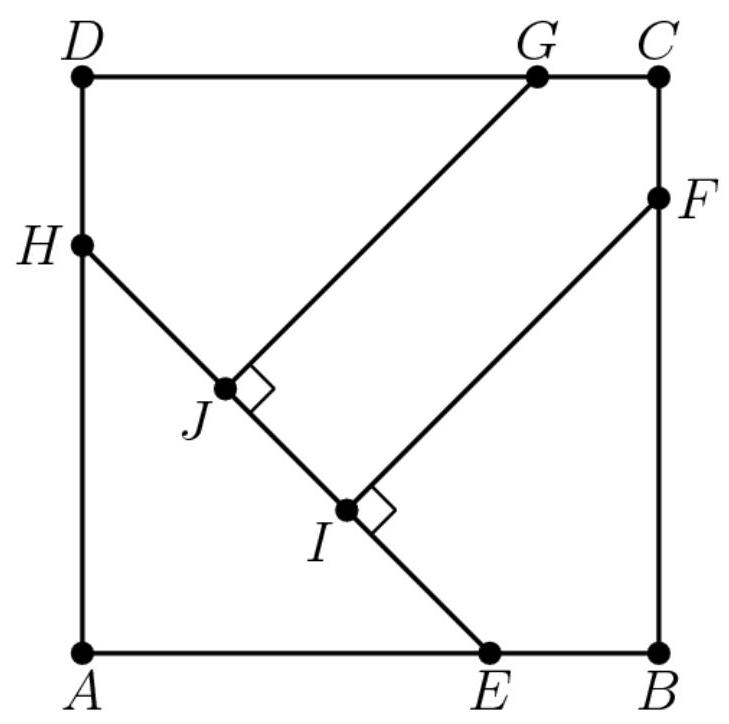
(A) \( \frac{7}{3} \) (B) \( 8 - 4\sqrt{2} \) (C) \( 1 + \sqrt{2} \) (D) \( \frac{7}{4}\sqrt{2} \) (E) \( 2\sqrt{2} \)
解答
由于总面积为4,正方形 \( {ABCD} \) 的边长为2。我们观察到,三角形 \( {HAE} \) 是一个面积为1的等腰直角三角形,因此可以确定边 \( {HA} \) 和 \( {AE} \) 均为 \( \sqrt{2} \) 。现在,考虑将 \( {FB} \) 和 \( {IE} \) 延长直至相交。设交点为 \( K \) 。我们注意到, \( E{BK} \) 也是一个以 \( 2 - \sqrt{2} \) 为边的等腰直角三角形,其面积为 \( 3 - \sqrt{2} \) 。接着,我们发现 \( {FIK} \) 同样是一个等腰直角三角形,其面积为 \( \frac{1}{2}F{I}^{2} \) 。该面积也等于 \( 1 + 3\underline{-2\sqrt{2}} \) 或 \( 4 - 2\sqrt{2} \) 。由于我们要求的是 \( F{I}^{2} \) ,因此需要取该值的两倍,即得到(B) \( 8 - 4\sqrt{2} \) 。~TLiu
解决方案 2
由于这是一个涉及边长的几何问题,且已知 \( {HE} \) 为2,我们可以用尺子量出 \( {FI} \) 与 \( {HE} \) 的比值。在试卷上测量, \( {HE} \) 约1.8英寸, \( {FI} \) 约1.4英寸。于是,我们将
\( {HE} \) 与 \( \frac{1.4}{1.8} \) 的比值,由此我们得到 \( {FI} = \frac{14}{9} \) 。我们取其平方得到 \( \frac{196}{81} \) ,最接近的答案就是 \( 88 - 4\sqrt{2} \) 。~Celloboy(注意,这只是我偶然使用并成功的一种策略。不要指望靠这个策略碰运气,因为它只是幸运猜测)
解决方案3
作辅助线 \( {AC} \) 。记 \( M \) 为其与 \( {HE} \) 的交点, \( N \) 为其与 \( {GF} \) 的交点。最后,记 \( x \) 为线段 \( {FN} \) , \( y \) 为线段 \( {FI} \) 。我们将为 \( x \) 和 \( y \) 建立两个方程,然后解出 \( {y}^{2} \) 。
由于 \( {ABCD} \) 的总面积为 \( 4 \Longrightarrow {AB} = 2 \) ,且 \( {AC} = 2\sqrt{2} \) 。此外, \( \bigtriangleup {AME} = \frac{1}{2} \Rightarrow {AM} = 1 \) 的面积为 \( \bigtriangleup {AME} = \frac{1}{2} \Rightarrow {AM} = 1 \) 。
关于 \( x \) 和 \( y \) 的两个方程分别为:
将第一个式子代入第二个式子,得到
\( \left\lbrack {\left( {2\sqrt{2} - 1}\right) - y}\right\rbrack \cdot \left\lbrack {\left( {2\sqrt{2} - 1}\right) + y}\right\rbrack = 1 \)
解得 \( {y}^{2} \) 为 \( 8\mathrm{\;B}8 - 4\sqrt{2} \sim \mathrm{{DrB}} \)
解决方案 4
作点 \( {F}^{\prime } \) 使 \( {F}^{\prime } \) 与 \( I \) 共线,并将直线 \( {FB} \) 延长至点 \( {B}^{\prime } \) ,使 \( {FI}{B}^{\prime }{F}^{\prime } \) 构成一个正方形。将直线 \( {AE} \) 延长与直线 \( {F}^{\prime }{B}^{\prime } \) 相交,点 \( {E}^{\prime } \) 为两线交点。该正方形面积等于 \( F{I}^{2} \) 。我们可见正方形 \( {ABCD} \) 的面积为4,即每边长为2。五边形 \( {EIF}{F}^{\prime }{E}^{\prime } \) 的面积为2。长度 \( {AE} = \sqrt{2} \) ,因此 \( {EB} = 2 - \sqrt{2} \) 。三角形 \( E{B}^{\prime }{E}^{\prime } \) 为等腰三角形,其面积为 \( \frac{1}{2}\left( {4 - 2\sqrt{2}}\right) \left( {2 - \sqrt{2}}\right) = 6 - 4\sqrt{2} \) 。将这两个面积相加,我们得到
\[ 2 + 6 - 4\sqrt{2} = 8 - 4\sqrt{2} \rightarrow \text{ (B) } \]
-OGBooger
解法5(高难度计算)
我们易见正方形 \( {ABCD} \) 的面积为4,边长为2,因为构成该正方形的四个区域面积均为1。延长 \( {FI} \) ,设其与 \( {AB} \) 的交点为 \( K \) 。连接 \( {AC} \) ,设 \( {AC} \) 与 \( {HE} \) 的交点为 \( L \) 。注意到三角形 \( A{EH} \) 的面积为1且 \( {AE} = {AH} \) 、 \( {AE} = {AH} = \sqrt{2} \) ,因此 \( {BE} = {HD} = 2 - \sqrt{2} \) 。设 \( {CG} = {GF} = m \) ,则 \( {BF} = {DG} = 2 - m \) 。又注意到 \( {KB} = {BE} = 2 - m \) ,于是
\( {KE} = {KB} - {BE} = 2 - m - \left( {2 - \sqrt{2}}\right) = \sqrt{2} - m \) 。现利用四边形 \( {BFIE} \) 的面积为1的条件,可列出如下方程:
\( \frac{1}{2}{\left( 2 - m\right) }^{2} - \frac{1}{4}{\left( \sqrt{2} - m\right) }^{2} = 1 \) 解方程得
\[ m = \frac{8 - 2\sqrt{2} - \sqrt{{64} - {32}\sqrt{2}}}{2}\text{. Now notice that} \]
\[ {FI} = {AC} - {AL} = 2\sqrt{2} - 1 - \frac{\sqrt{2}}{2} * \frac{8 - 2\sqrt{2} - \sqrt{{64} - {32}\sqrt{2}}}{2} \]
\[ = 2\sqrt{2} - 1 - \frac{8\sqrt{2} - 4 - \sqrt{{128} - {64}\sqrt{2}}}{4} = \frac{\sqrt{{128} - {64}\sqrt{2}}}{4}\text{. Hence} \]
\[ F{I}^{2} = \frac{{128} - {64}\sqrt{2}}{16} = 8 - 4\sqrt{2}\text{. -HarryW} \]
2020 AMC 10B 试题/第22题
题目
求 \( {2}^{202} + {202} \) 除以 \( {2}^{101} + {2}^{51} + 1 \) 的余数?
(A) 100 (B) 101 (C) 200 (D) 201 (E) 202 解法
设 \( x = {2}^{50} \) 。现求 \( \frac{4{x}^{4} + {202}}{2{x}^{2} + {2x} + 1} \) 的余数。
我们可用多项式除法,但分母与Sophie Germain恒等式(Sophie Germain Identity)极为相似,该恒等式表述为
\[ {a}^{4} + 4{b}^{4} = \left( {{a}^{2} + 2{b}^{2} + {2ab}}\right) \left( {{a}^{2} + 2{b}^{2} - {2ab}}\right) \]
令 \( a = 1 \) 与 \( b = x \) ,则有
\[ 1 + 4{x}^{4} = \left( {1 + 2{x}^{2} + {2x}}\right) \left( {1 + 2{x}^{2} - {2x}}\right) \]
整理后可见这正是我们所需:
\[ \frac{4{x}^{4} + 1}{2{x}^{2} + {2x} + 1} = 2{x}^{2} - {2x} + 1 \]
于是
\[ \frac{4{x}^{4} + {202}}{2{x}^{2} + {2x} + 1} = \frac{4{x}^{4} + 1}{2{x}^{2} + {2x} + 1} + \frac{201}{2{x}^{2} + {2x} + 1} \]
由于前半部分已整除,余数必为
(D) 201 ~quacker88
解决方案 2
与解法1类似,设 \( x = {2}^{50} \) 。只需找出 \( \frac{4{x}^{4} + {202}}{2{x}^{2} + {2x} + 1} \) 的余数。
多项式除法所得余数为(D) 201
MAA原始解法
\[ {2}^{202} + {202} = {\left( {2}^{101}\right) }^{2} + 2 \cdot {2}^{101} + 1 - 2 \cdot {2}^{101} + {201} \]
\[ = {\left( {2}^{101} + 1\right) }^{2} - {2}^{102} + {201} \]
\[ = \left( {{2}^{101} - {2}^{51} + 1}\right) \left( {{2}^{101} + {2}^{51} + 1}\right) + {201}\text{.} \]
因此,我们看到余数必定是(D) 201
2020 AMC 10B 试题/第23题
问题
坐标平面中的正方形 \( {ABCD} \) 的顶点位于点 \( A\left( {1,1}\right) , B\left( {-1,1}\right) , C\left( {-1, - 1}\right) , \) 和 \( D\left( {1, - 1}\right) . \) 。考虑以下四种变换: \( L, \) 绕原点逆时针旋转 \( {90}^{ \circ } \) ; \( R, \) 绕原点顺时针旋转 \( {90}^{ \circ } \) ; \( H, \) 关于 \( x \) 轴的反射;以及 \( V, \) 关于 \( y \) 轴的反射。
这些变换中的每一个都将正方形映射到自身,但标记顶点的位置会发生变化。例如,先应用 \( R \) 再应用 \( V \) ,会把位于(1,1)的顶点 \( A \) 送到(-1,-1),而把位于(-1,1)的顶点 \( B \) 留在原位。从 \( \{ L, R, H, V\} \) 中选取20个变换组成的序列,有多少种能把所有标记顶点送回原始位置?(例如, \( R, R, V, H \) 就是一个由4个变换组成的序列,它能把顶点送回原始位置。)
(A) \( {2}^{37} \) (B) \( 3 \cdot {2}^{36} \) (C) \( {2}^{38} \) (D) \( 3 \cdot {2}^{37} \) (E) \( {2}^{39} \)
解决方案
用(+)表示逆时针/起始方向,用(-)表示顺时针方向。用1、2、3、4表示 \( A \) 所在的象限。
要认识到,无论从哪个奇象限、以何种朝向出发,这4种变换最终都会得到 \( \left( {2+,2-,4+,4 - }\right) \) 的某种排列。
同样地,从任意偶象限和任意方向出发,这4种变换都会得到 \( \left( {1+,1-,3+,3 - }\right) \) 的某种排列。
前19步我们随意行动,每一步都有4种选择。由于19是奇数,我们最终必定落在偶象限。
如上所述,我们知道四种变换中恰好有一种会给出 \( \left( {1 + }\right) \) ,我们必须使用该变换。
因此 \( {4}^{19} = \left( C\right) {2}^{38} \)
解法2
希望有人能想出更好的办法,但这里给出一个间接答案,仅在你实在走投无路时使用。可以走20步,每步有4种选择,因此总共有 \( {4}^{20} = {2}^{40} \) 种走法。首先,20步之后,点A只能位于第一象限(1,1)或第三象限(-1,-1)。只有第一象限的情况有效,所以除以2。接下来,C必须与A位于相反的象限。B可以位于第二 \( \left( \left( {-1,1}\right) \right) \) 或第四象限 \( \left( \left( {1, - 1}\right) \right) \) ,但我们希望它在第二象限,于是再除以2。此时A和B已满足条件,C和D也会回到原位。 \( \frac{{2}^{40}}{2 \cdot 2} = {2}^{38} \) 。答案是 \( C \) -Kinglogic
解法3
序列总数为 \( {4}^{20} = {2}^{40} \) 。
注意,反射次数只能为偶数,因为它们会使顶点 \( A, B, C, D \) 保持相同的逆时针方向。因此,变换后仍保持与原排列相同逆时针方向的概率为 \( \frac{1}{2} \) 。接下来,偶数次反射意味着旋转次数也必须是偶数,因为它们的和为偶数。偶数次旋转只能得到原位或 \( {180}^{ \circ } \) 旋转后的位置。
由于旋转 \( R \) 与旋转 \( L \) 相互抵消,它们的数量差决定最终位置。在已知旋转次数为偶数的条件下,变换使顶点回到原位的概率等价于
\[ \left| {n\left( R\right) - n\left( L\right) }\right| \equiv 0\left( {\;\operatorname{mod}\;4}\right) \text{when} \]
\[ \left| {n\left( H\right) - n\left( V\right) }\right| \equiv 0{\;(\operatorname{mod}\;4)} \]
\[ \left| {n\left( R\right) - n\left( L\right) }\right| \equiv 2{\;(\operatorname{mod}\;4)}\text{when} \]
\[ \left| {n\left( H\right) - n\left( V\right) }\right| \equiv 2{\;(\operatorname{mod}\;4)} \]
再次得到 \( \frac{1}{2} \) 。
因此, \( {2}^{40} \cdot \frac{1}{2} \cdot \frac{1}{2} = 0 = 0{2}^{38} \sim \) joshuamh111 解法4
注意到,任意一对这样的变换要么交换 \( x \) 和 \( y \) 坐标,要么对 \( x \) 和 \( y \) 坐标取反,要么既交换又取反,要么保持原样不变。进一步观察,对于每一种结果,若再施加一对变换,上述四种结果之一会再次出现,且概率相等。因此,无论前19对变换后处于何种状态,最后一对变换有 \( \frac{1}{4} \) 的概率使图形回到原位。于是答案为
\[ \frac{{4}^{20}}{4} = {4}^{19} = {(C}{2\;2}^{38} \]
2020 AMC 10B 试题/第24题
题目
有多少个正整数 \( n \) 满足
\[ \frac{n + {1000}}{70} = \lfloor \sqrt{n}\rfloor ? \]
(回忆: \( \lfloor x\rfloor \) 表示不超过 \( x \) 的最大整数。)
(A) 2 (B) 4 (C) 6 (D) 30 (E) 32
解答
首先注意到 \( \left( {x + {1000}}\right) /{70} \) 和 \( \sqrt{n} \) 的图像在两个点相交。然后, \( \left( {n + {1000}}\right) /{70} \) 必须是整数。这意味着n与 \( {50}{\;(\operatorname{mod}\;{70})} \) 同余。
对于第一个交点,测试 \( n \) 的前几个值(每次给 \( n \) 加70并注意到左侧每次增加1)得到 \( n = {20} \) 和 \( n = {21} \) 。通过图像估算可缩小其他情况,即 \( n = {47} \) 和 \( n = {50} \) 。总共有6种情况,答案为(C) 6。
~DrJoyo
解法2(作图法)
一种直观的解题方法是作图。显然,你需要知道平方根函数的图像长什么样,并且如果某个函数被取整(即取不大于该值的最大整数),图像会呈现阶梯状。另一个函数只是一条斜率为 \( 1/{70} \) 的直线。如果你精确地画出平方函数导数接近线性函数导数的两个区域,就可以推断出有3个交点值靠近阶梯的左侧,另外3个交点值靠近阶梯的右侧。
通过细致的作图,你会发现答案是(C,6)
下方链接提供了带有交点的详细图像:https://www.desmos.com/calculator/e5wk9adbuk
解法3
- 不可靠且不深入的解法(适合猜答案的学生)
我们可以先考虑不含取整函数的方程:
\[ \frac{n + {1000}}{70} = \sqrt{n} \]
两边同乘70后再平方:
\[ {n}^{2} + {2000n} + {1000000} = {4900n} \]
将所有项移到左边:
\[ {n}^{2} - {2900n} + {1000000} = 0 \]
现在可以通过"愿望思维"来确定因式:
\[ \left( {n - {400}}\right) \left( {n - {2500}}\right) = 0 \]
这意味着当 \( n = {400} \) 和 \( n = {2500} \) 时,不含取整函数的方程成立。
现在只需在原方程中检验400和2500附近70的倍数:
当 \( n = {330} \) 时,左边 \( = {19} \) 但 \( {18}^{2} < {330} < {19}^{2} \) 所以右边 \( = {18} \)
当 \( n = {400} \) 时,左边 \( = {20} \) 且右边 \( = {20} \)
当 \( n = {470} \) 时,左边 \( = {21} \) 且右边 \( = {21} \)
对于 \( n = {540} \) ,左侧=22但 \( {540} > {23}^{2} \) ,因此右侧=23
现在我们转到 \( n = {2500} \)
对于 \( n = {2430} \) ,左侧=49且 \( {49}^{2} < {2430} < {50}^{2} \) ,因此右侧=49
对于 \( n = {2360} \) ,左侧=48且 \( {48}^{2} < {2360} < {49}^{2} \) ,因此右侧=48
对于 \( n = {2290} \) ,左侧=47且 \( {47}^{2} < {2360} < {48}^{2} \) ,因此右侧=47
对于 \( n = {2220} \) ,左侧=46但 \( {47}^{2} < {2220} \) ,因此右侧=47
对于 \( n = {2500} \) ,左侧 \( = {50} \) 且右侧 \( = {50} \)
对于 \( n = {2570} \) ,左侧=51但 \( {2570} < {51}^{2} \) ,因此右侧=50
因此总共有6个解, \( n = {400},{470},{2290},{2360},{2430},{2500} = (\mathrm{C} \) )6
解法4
这是我第一次在此发布解法,如有错误请见谅。
已知
\[ \frac{n + {1000}}{70} = \lfloor \sqrt{n}\rfloor \]
\( \lfloor \sqrt{n}\rfloor \) 必须为整数,这意味着 \( n + {1000} \) 可被70整除。由于 \( {1000} \equiv {20}{\;(\operatorname{mod}\;{70})} \) ,这意味着 \( n \equiv {50}{\;(\operatorname{mod}\;{70})} \) ,因此我们可以将 \( n = {70k} + {50} \) 写成 \( k \in \mathbb{Z} \) 。
因此,
\[ \frac{n + {1000}}{70} = \frac{{70k} + {1050}}{70} = k + {15} = \lfloor \sqrt{{70k} + {50}}\rfloor \]
此外,我们可以说 \( \sqrt{{70k} + {50}} - 1 \leq k + {15} \) 和 \( k + {15} \leq \sqrt{{70k} + {50}} \)
将第二个不等式平方,我们得到
\( {k}^{2} + {30k} + {225} \leq {70k} + {50} \Rightarrow {k}^{2} - {40k} + {175} \leq 0 \Rightarrow \left( {k - 5}\right) \left( {k - {35}}\right) \leq 0 \Rightarrow 5 \leq k \)
类似地,解第一个不等式得到 \( k \leq {19} - \sqrt{155} \) 或 \( k \geq {19} + \sqrt{155} \)
\( \sqrt{155} \) 略大于12,因此我们可以写成 \( k \leq 6 \) 或 \( k \geq {32} \) 。
将其与 \( 5 \leq k \leq {35} \) 结合,我们得到 \( k = 5,6,{32},{33},{34},{35} \) 都是使 \( n \) 有有效解的 \( k \) 的解,因此答案为 \( \mathbf{\left( C\right) 6} \) 。
-Qqqwerw解答
解法5
我们从给定方程开始
\[ \frac{n + {1000}}{70} = \lfloor \sqrt{n}\rfloor \]
由此,我们可以从一般不等式 \( \lfloor \sqrt{n}\rfloor \leq \sqrt{n} < \lfloor \sqrt{n}\rfloor + 1 \) 入手。这意味着
\[ \frac{n + {1000}}{70} \leq \sqrt{n} < \frac{n + {1070}}{70} \]
分别解每个不等式得到两个不等式:
\[ n - {70}\sqrt{n} + {1000} \leq 0 \rightarrow \left( {\sqrt{n} - {50}}\right) \left( {\sqrt{n} - {20}}\right) \leq 0 \rightarrow {20} \leq \sqrt{n} \leq {50} \]
\[ n - {70}\sqrt{n} + {1070} > 0 \rightarrow \sqrt{n} < {35} - \sqrt{155},\sqrt{n} > {35} + \sqrt{155} \]
化简并近似小数后,一个不等式有2个解,另一个有4个解。因此 \( 2 + 4 = \) (C)6
~Rekt4
2020 AMC 10B试题/第25题
题目
设 \( D\left( n\right) \) 表示将正整数 \( n \) 写成乘积的方式数
\[ n = {f}_{1} \cdot {f}_{2}\cdots {f}_{k}, \]
其中 \( k \geq 1 \) , \( {f}_{i} \) 为严格大于1的整数,且因子的顺序不同视为不同(即仅因子顺序不同的两种表示计为不同)。例如,数字6可写成6、 \( 2 \cdot 3 \) 和 \( 3 \cdot 2 \) ,因此 \( D\left( 6\right) = 3 \) 。 \( D\left( {96}\right) \) 是多少?
(A)112(B)128(C)144(D)172(E)184
解答
注意 \( {96} = {2}^{5} \cdot 3 \) 。由于最多有六个不一定不同的因子 \( > 1 \) 相乘得96,我们有六种情况: \( k = 1,2,...,6. \) 现在我们逐一查看这六种情况。
\( k = 1 \) :我们看到只有1种方式,即96本身。
\( k = 2 \) :这样,我们有一个位置放3,另一个位置放2,并且考虑对称性。其余四个2给我们5种方式,对称性再翻倍,因此共有10种。
\( k = 3 \) :我们以3,2,2为基准。需要在3个位置再乘2,并发现剩余的三个2的幂次可以按3-0-0、2-1-0或1-1-1分配。3-0-0分配有 \( 6 + 3 = 9 \) 种方式(24-2-2及其对称;2-3-16及其对称),2-1-0分配有 \( 6 \cdot 3 = {18} \) 种方式(因所有位置不同),1-1-1分配有3种方式(6-4-4及其对称),因此本情况共有 \( 9 + {18} + 3 = {30} \) 种方式。
\( k = 4 \) :我们以3,2,2,2为基准,其余两个2的分配为2-0-0-0或1-1-0-0。前者提供 \( 4 + {12} = {16} \) 种方式(12-2-2-2及其对称和3-8-2-2及其对称),后者也提供 \( {12} + {12} = {24} \) 种方式(6-4-2-2及其对称和3-4-4-2及其对称),总计 \( {16} + {24} = {40} \) 种方式。
\( k = 5 \) :我们以3,2,2,2,2为基准,最后一个2可放在另一个2上或放在3上。放在3上因对称性有5种方式,放在另一个2上因对称性有 \( 5 \cdot 4 = {20} \) 种方式。因此共有 \( 5 + {20} = {25} \) 种方式。
\( k = 6 \) :我们有3,2,2,2,2,2且考虑对称性,没有更多2可乘,故因对称性共有6种方式。
因此,相加后我们得到 \( 1 + {10} + {30} + {40} + {25} + 6 = \) (A)112
~kevinmathz
解法2
如前所述,注意 \( {96} = {2}^{5} \cdot 3 \) ,我们需要考虑6种不同情况,对应分解中因子个数 \( k \) 的每一种可能值。然而,我们不再逐一查看,而是寻找具有 \( k \) 个因子的分解总数的一般形式。首先,分解中必须包含一个本身是3的倍数的因子,有 \( k \) 种选择,其余因子必须至少含一个2的因子。接下来,考虑剩余的 \( 6 - n \) 个2的因子要分配到 \( k \) 个因子中。使用隔板法,分配方式数为
\[ \left( \begin{matrix} \left( {6 - k}\right) + k - 1 \\ 6 - k \end{matrix}\right) = \left( \begin{matrix} 5 \\ 6 - k \end{matrix}\right) \]
这使得对于每个 \( \mathrm{k} \) 共有 \( k\left( \begin{matrix} 5 \\ 6 - k \end{matrix}\right) \) 种可能。
为得到分解总数,将所有可能的 \( k \) 值相加:
\[ \mathop{\sum }\limits_{{k = 1}}^{6}k\left( \begin{matrix} 5 \\ 6 - k \end{matrix}\right) = 1 + {10} + {30} + {40} + {25} + 6 = 6 \]
解法3
首先考察 \( {f}_{1} \) 。 \( {f}_{1} \) 可以取96除1外的任何因数。对于每一个 \( {f}_{1} \) 的选择,所得 \( {f}_{2}\ldots {f}_{k} \) 的乘积必须为 \( {96}/{f}_{1} \) 。这意味着,对于每个 \( {f}_{1} \) ,其余 \( {f}_{a},1 < a < = k \) 按题述方案书写的方式数等于 \( D\left( {{96}/{f}_{1}}\right) \) ,因为仅当 \( {f}_{1} \cdot x = {96} \) 且乘积 \( x \) 的因子均大于1,且不同顺序的乘积分别计数时, \( {f}_{2} \cdot {f}_{3} \) … \( \cdot {f}_{k} = x \) 的乘积才被计为一个有效乘积。
例如,设第一个因子为2,则剩余数必须乘得48,于是以2开头的乘积书写方式数为 \( D\left( {48}\right) \) 。为累加所有可能起始因子对应的解数,需计算并求和 \( D\left( {{96}/{f}_{1}}\right) \) 对所有可能的 \( {f}_{1} \) ,但排除96和1,因为按题意单个1不计。然而96被计入,但仅产生1种可能,即首因子且唯一因子为96。这意味着
\[ D\left( {96}\right) = D\left( {48}\right) + D\left( {32}\right) + D\left( {24}\right) + D\left( {16}\right) + D\left( {12}\right) + D\left( 8\right) + D\left( 6\right) + D\left( 4\right) + D\left( 3\right) + D\left( 2\right) \]
与其先对大因子计算D,不如将 \( D\left( {48}\right) \) 、 \( D\left( {32}\right) \) 和 \( D\left( {24}\right) \) 化简为 \( D\left( m\right) \) 的和,其中 \( m < = {16} \) ,以简化计算。依递归定义 \( D\left( n\right) = ( \) 为 \( D\left( c\right) ) + 1 \) 的和,其中c遍历 \( n \) 除1与其本身外的所有因数,该和化简为
\[ D\left( {96}\right) = \left( {D\left( {24}\right) + D\left( {16}\right) + D\left( {12}\right) + D\left( 8\right) + D\left( 6\right) + D\left( 4\right) + D\left( 3\right) + D\left( 2\right) + 1}\right) + \]
\( \left( {D\left( {16}\right) + D\left( 8\right) + D\left( 4\right) + D\left( 2\right) + 1}\right) + D\left( {24}\right) + D\left( {16}\right) + D\left( {12}\right) + D\left( 8\right) + D\left( 6\right) + D\left( 4\right) + D \)
\( D\left( {24}\right) = D\left( {12}\right) + D\left( 8\right) + D\left( 6\right) + D\left( 4\right) + D\left( 3\right) + D\left( 2\right) + 1 \) ,于是该和进一步化简为
\( D\left( {96}\right) = {3D}\left( {16}\right) + {4D}\left( {12}\right) + {5D}\left( 8\right) + {4D}\left( 6\right) + {5D}\left( 4\right) + {4D}\left( 3\right) + {5D}\left( 2\right) + 5 \) ,合并同类项后。通过快速分类讨论,
\( D\left( {16}\right) = 8, D\left( {12}\right) = 8, D\left( 8\right) = 4, D\left( 6\right) = 3, D\left( 4\right) = 2, D\left( 3\right) = 1 \) 和 \( D\left( 2\right) = 1 \) 。将这些值代入上式,
\[ D\left( {96}\right) = 3 \cdot 8 + 4 \cdot 8 + 5 \cdot 4 + 4 \cdot 3 + 5 \cdot 2 + 4 \cdot 1 + 5 \cdot 1 + 5 = \text{(A) 112} \]
~monmath 又名 Fmirza
解法4
注意 \( {96} = 3 \cdot {2}^{5} \) ,且一个素数完全幂的 \( D \) 相对容易计算。还请注意,可通过统计将3插入乘积为32的数集的所有方式数,由 \( D\left( {32}\right) \) 求得 \( D\left( {96}\right) \) 。
首先,计算 \( D\left( {32}\right) \) 。由于 \( {32} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \) ,你只需找出将2分成若干组的方法数,使得每组至少有一个2。根据隔板法(stars and bars),这会产生:含五项的1种方式,含四项的4种方式,含三项的6种方式,含两项的4种方式,以及含一项的1种方式。(总数16在后续计算中并不需要。)
然后,为了得到 \( D\left( {96}\right) \) ,在每一种可能的 \( D\left( {32}\right) \) 序列中,插入一个3:可以把它放在原数字的旁边(有 \( n + 1 \) 种方式,其中 \( n \) 为该 \( D\left( {32}\right) \) 序列的项数),或者把其中一个数字乘以3(有 \( n \) 种方式)。这样,含一项的有 \( 2 + 1 = 3 \) 种方式,含两项的有 \( 3 + 2 = 5 \) 种方式,含三项的有7种,含四项的有9种,含五项的有11种。
由此得到的序列总数为 \( 3 \cdot 1 + 5 \cdot 4 + 7 \cdot 6 + 9 \cdot 4 + {11} \cdot 1 = \) (A)112 ~emerald_block